
We can therefore use the F-test (see Two Sample Hypothesis Testing of Variances) to determine whether or not to reject the null hypothesis. Thus the null hypothesis becomes equivalent to H 0: σ B = σ W (or in the one-tail test, H 0: σ B ≤ σ W). In conclusion, if the null hypothesis is true, and so the population means μ j for the k groups are equal, then any variability of the group means around the total mean is due to chance and can also be considered an error. If the null hypothesis is false we expect that F > 1 since MS B will estimate the same quantity as MS Wplus group effects. If the null hypothesis is true then MS W and MS B are both measures of the same error and so we should expect F = MS B / MS W to be around 1. While if the alternative hypothesis is true, then α j ≠ 0, and so If the null hypothesis is true, then α j = 0, and so For this reason, we will sometimes replace MS W, SS Wand df W by MS E, SS Eand df E. MS W is a measure of the variability of each group around its mean, and, by Property 3, can be considered a measure of the total variability due to error. Observation: MS Bis a measure of the variability of the group means around the total mean. Observation: Click here for a proof of Property 1, 2 and 3. the mean of the group means is the total mean. If all the groups are equal in size, say n j = m for all j, then As before we have the sample version x ij = x̄ + a j + e ij where e ij is the counterpart to ε ij in the sample.Īlso ε ij = x ij – (μ + α j) = x ij – μ jand similarly, e ij = x ij – x̄ j. Similarly, we can represent each element in the sample as x ij = μ + α j + ε ij where ε ijdenotes the error for the ith element in the jth group.
We have a similar estimate for the sample of x̄ j = x̄ + a j. the departure of the jth group mean from the total mean). First, we estimate the group means from the total mean: = μ + a jwhere a jdenotes the effect of the jth group (i.e. Property 1: If a sample is made as described in Definition 1, with the x ijindependently and normally distributed and with all σ j 2equal, thenĭefinition 2: Using the terminology from Definition 1, we define the structural model as follows. MS Bis the variance for the “between sample” i.e. MS W is the weighted average of the group sample variances (using the group df as the weights). Observation: Clearly MS T is the variance for the total sample.
We also define the following degrees of freedom the weighted sum of the squared deviations of the group means from the grand mean. SS B is the sum of the squares between-group sample means, i.e. the sum of the squared means across all groups. SS W is the sum of squares within the groups, i.e. the sum of the squared deviations from the grand mean. SS T is the sum of squares for the total sample, i.e. Let the sum of squares for the jth group be We will use the abbreviation x̄ j for the mean of the jth group sample (called the group mean) and x̄ for the mean of the total sample (called the total or grand mean). We will use the index i for these.Īnd so the total sample consists of all the elements The sample elements are the rows in the analysis. Each group consists of a sample of size n j.

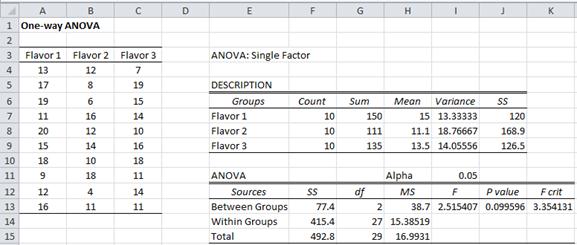
We interrupt the analysis of this example to give some background, after which we will resume the analysis.ĭefinition 1: Suppose we have k samples, which we will call groups (or treatments) these are the columns in our analysis (corresponding to the 3 flavors in the above example). Our null hypothesis is that any difference between the three flavors is due to chance. Determine whether there is a perceived significant difference between the three flavorings. Each person is then given a questionnaire that evaluates how enjoyable the beverage was. Group 1 tastes flavor 1, group 2 tastes flavor 2 and group 3 tastes flavor 3. We begin with an example which is an extension of Example 1 of Two Sample t-Test with Equal Variances.Įxample 1: A marketing research firm tests the effectiveness of three new flavorings for a leading beverage using a sample of 30 people, divided randomly into three groups of 10 people each. We will define the concept of factor elsewhere, but for now, we simply view this type of analysis as an extension of the t-tests that are described in Two Sample t-Test with Equal Variances and Two Sample t-Test with Unequal Variances.


 0 kommentar(er)
0 kommentar(er)
